И.A. Курилин
«ТЕОРИЯ ПОЛЕЙ ВРЕМЕНИ» как реализация программы Эйнштейна по поиску геометрии для построения теории единого грави-электромагнитного поля
Предлагаемая вниманию работа содержит реализацию программы А. Эйнштейна по поиску подходящей геометрической модели, позволяющей осуществить подход к вопросу описания гравитации и электромагнетизма на основе введения на четырехмерном многообразии двух геометрических структур: дефинитной метрики Римана (задающей знакоопределенную квадратную форму на векторах) и несимметричной аффинной связности, на которые дополнительно накладывается условие согласованности в форме теоремы Э. Шредингера.
I.A. Kurilin
“TIME FIELD THEORY” as the implementation of Einstein’s program on the search for geometry for constructing the theory of united gravi-electromagnetic field
The proposed work contains the implementation of Einstein’s program to search the suitable geometric model, which enables to carry out an approach to a question of gravity description and electromagnetism on the basis of introduction on the four-dimensional variety of two geometric structures: the definite certificate of Riemann (assigning the definite square shape on the vectors) and asymmetrical affine connectedness on which additionally is superimposed the condition of the coordination in the form of Schrцdinger’s theorem.
Сам Эйнштейн понимал, что его пространство на самом
деле может оказаться неадекватным, потому что совсем
по-разному включает гравитационное поле и поле электромагнитное…
Построение пространства, которое объединило бы гравитационное
и электромагнитное поле, до сих пор остается одной
из фундаментальных проблем физики.
П.А.М. Дирак
К сожалению, точка зрения одного из основоположников современной физики не является в наши дни популярной. Напротив, любые работы в этом направлении, в лучшем случае, рассматриваются как рассчитанные на эпатаж обывателя выходки «чудаковатых ниспровергателей истин» [4], в худшем случае – как злонамеренные попытки дискредитации современной науки. Не вступая в бесплодную полемику на эту «околонаучную» тему, попытаемся в рамках ограниченного формата настоящей статьи сформулировать основополагающие принципы нового подхода к построению Единой теории поля, которые кардинально меняют современные общепринятые представления о структуре пространства-времени, и приведем основные результаты, которые удалось получить исходя из этих инновационных идей. По необходимости изложение материала будет предельно сжатым.
Прежде всего, сформулируем задачу: «Возможно ли в рамках общерелятивистской методологии предложить геометрию, которая позволила бы путем естественного и прозрачного обобщения идей этой методологии прийти к описанию гравитации и электромагнетизма (хотя бы чисто формально) как единого поля, и конкретно – поля несимметричной афинной связности». При этом предполагается, что в конечном итоге мы должны получить естественное обобщение общерелятивистской модели, хотя бы в смысле включения полевых уравнений последней в уравнения «Единого поля» в качестве очевидного частного случая.
Хотелось бы также исключить те негативные моменты, отмеченные еще самим Альбертом Эйнштейном в его работах по единой теории поля [4], с которыми сталкивались все, кто предпринимал попытки решения подобной задачи и, которые, по мнению Эйнштейна, не позволяют признать их успешными в виду исключительной сложности уравнений теории, делающей практически невозможным сколь-нибудь законченный и подробный анализ физического содержания теории и, следовательно, не дающей возможности предложить эксперименты по ее проверке.
Итак, предлагаемая вниманию работа содержит реализацию программы А. Эйнштейна по поиску подходящей геометрической модели, позволяющей осуществить подход к вопросу описания гравитации и электромагнетизма на основе введения на четырехмерном многообразии двух геометрических структур: дефинитной метрики Римана (задающей знакоопределенную квадратичную форму на векторах) и несимметричной афинной связности, на которые дополнительно накладывается условие согласованности в форме теоремы Э. Шредингера [1]. Это формализованное математическое содержание теории будет далее представлено в виде УРАВНЕНИЙ ПОЛЯ, получаемых из соответствующего вариационного принципа.
Полученная на этом пути теория, которую всюду далее будем обозначать по первым буквам ее названия ТПВ, не может быть сведена ни к одной из ранее рассматривавшихся в специальной литературе теорий (симметричная теория Вейля, несимметричная теория Эйнштейна – Штрауса, чисто афинная теория Эддингтона – Эйнштейна и др.) и не является их модификацией или частным случаем. C другой стороны, эйнштейновская теория относительности 1915 г. (ОТО) сама может рассматриваться как весьма специальный частный случай предлагаемой теоретической схемы. Последнее, в частности, означает, что уравнения поля предлагаемой теории при одном дополнительном упрощающем предположении могут быть приведены к виду уравнений эйнштейновской ОТО с «космологическим лямбда-членом» и полностью геометризированной правой частью.
Выбранное автором название теории – «Теория полей времени» (ТПВ) – наиболее точно и полно отражает физическую суть и содержание предлагаемой теоретической модели. С обсуждения этих физических оснований новой теории (которые традиционно являются предметом специальной теории относительности – СТО) мы и начнем.
В качестве исходного отправного постулата предлагается исходить из следующего:
A. Физическое пространство – суть четырехмерное пространство (4-пространство) однородное и изотропное по всем четырем направлениям. Последнее, очевидно, полностью исключает идею о так называемой «Стреле времени».
B. Любое движение (т. е. распространение любого сигнала) в 4-пространстве происходит с постоянной скоростью, равной по величине скорости распространения света в вакууме.
Чтобы «зрительно» представить смысл сформулированных постулатов приведем схему, изображающую структуру 4-пространства, в виде совокупности четырех трехмерных подпространств («3-пространств»), для каждого из которых задано свое собственное направление оси времени соответственно вдоль одной из координатных осей: x0, x1, x2 , x3 фиксированной системы координат {xk} (рис. 1):
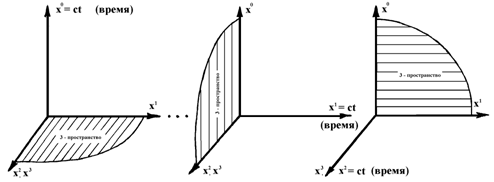
Рис. 1
На диаграмме (рис. 2) изображено преобразование {x’k} «штрихованной» системы координат, движущейся со скоростью V вдоль оси x1 исходной системы координат {xk}, а диаграмма (рис. 3) иллюстрирует «Закон сложения скоростей» для простейшего случая.
Итак, смысл сформулированных постулатов сводится к следующему:
1. В каждой точке 4-пространства всегда можно рассматривать четыре различных системы отсчета, движущиеся друг относительно друга с постоянной скоростью (равной скорости света в вакууме) во взаимно-ортогональных направлениях. Направление движения системы отсчета определяет в каждой точке 4-пространства направление локального для этой системы времени. По сути, эти системы отсчета представляют собой ни что иное, как четыре взаимно ортогональных трехмерных физических пространства, в каждом из которых его локальное время ортогонально направлению локального времени трех остальных трехмерных пространств.
Разделены эти пространства некоторой условной границей, которую можно по устоявшейся традиции продолжать называть «световым конусом». На диаграмме (рис. 2) эта граница – световой конус – обозначена линиями L и отделяет 3-пространство с временной осью х0 от ортогонального 3-пространства с локальным временем, направленным вдоль оси х1. В отличие от эйнштейновсой СТО геодезические линии на «световом конусе» НЕ НУЛЕВЫЕ! Это определяется тем, что метрика пространства – времени – Дефинитна (т. е. задается знакоопределенной квадратичной формой на векторах и по этой причине не обращающейся в ноль ни в какой точке 4-пространства). В свою очередь, дефинитность метрики означает необходимость замены группы Лоренца группой действительных вращений четырехмерного пространства, относительно которой уравнения электродинамики также ковариантны. Именно это преобразование координат изображено на диаграммах (рис. 2) и (Рис. 3).
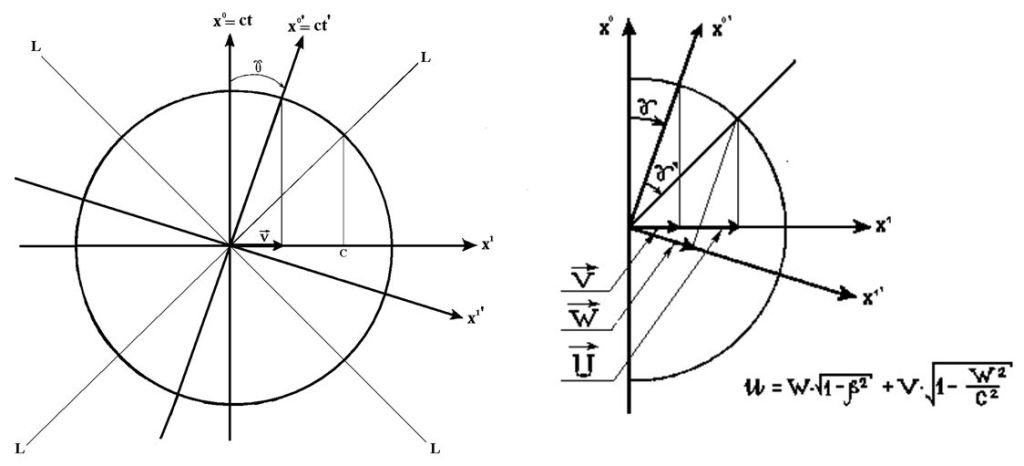
Рис. 2 Рис. 3
2. Легко понять, что граница «светового конуса» не является непреодолимым барьером для частицы, находящейся в системе отсчета {xk} с локальным временем х0 (как, например, это имеет место в эйнштейновской ОТО). Очевидно, что по достижении частицей определенного значения скорости в системе отсчета {xk}, направление ее собственного времени отклонится от направления времени системы отсчета (ось х0) на угол больший (или равный) 450, и с этого момента материальная частица окажется в ДРУГОМ трехмерном пространстве, время в котором направлено вдоль оси х1. Естественно, что для наблюдателя в исходной системе отсчета с локальным временем х0 эта частица перестает быть наблюдаемой как физическое тело, но, разумеется, нет никаких оснований полагать, что само это материальное тело прекратило свое физическое существование.
Необходимо заметить, что приведенное здесь описание следует рассматривать как «первое приближение» к реально имеющей место ситуации. Ограниченный размер настоящей статьи не предполагает детального рассмотрения этого вопроса. Более того, нет возможности обсудить исключительной важности вопрос о непротиворечивости предложенной схемы современным экспериментальным данным. Этому вопросу следовало бы посвятить отдельную работу, объем которой многократно превысил бы объем исходной статьи по «Теории полей времени». Коротко отметим лишь главное:
a. Интерпретация опытных данных сама по себе является сложной проблемой и, как показано в книге [2] Макса Джеммера: «сама может быть неоднозначной даже в рамках принятой теоретической схемы» (здесь имеется в виду эйнштейновская СТО). Позволю себе предостеречь опонентов от легковесных заявлений в духе анонимного рецензента из редакции журнала «Теоретическая и математическая физика»: «Замена группы Лоренца на группу действительных вращений четырехмерного пространства в этом случае привела бы к противоречащим эксперименту законам преобразования таких физических величин, как энергия и импульс частиц, напряженностей электромагнитного поля и др.». Хотелось бы спросить этого рецензента, готов ли он назвать хоть один эксперимент (авторов эксперимента, время проведения опытов, описание установки и оборудования, суть проводимых измерений, точность полученных результатов и т. д.) и с карандашом в руках доказать, что его результаты опровергают выводы ТПВ. Напротив, автор настоящей статьи утверждает, что все известные ему экспериментальные результаты могут быть непротиворечивым и вполне удовлетворительным образом интерпретированы с точки зрения ТПВ.
б. Автор готов предложить «решающий эксперимент» по проверке исходных принципов ТПВ, позволяющий однозначно и бесповоротно либо опровергнуть их правомерность, а следовательно и принятую пространственно-временную модель ТПВ, либо напротив доказать ее правильность. Принципиально важным при этом является то обстоятельство, что такой эксперимент легко осуществим средствами современной экспериментальной физики, поскольку не связан с сильными полями гравитации и даже не является гравитационным экспериментом. Дело в том, что ТПВ вполне однозначно предсказывает для «продольного эффекта Доплера» (именно для продольного, а не поперечного, который только и изучался в опытах Айвса – Стилуэлла в 1938, а затем в 1941 г. в рамках экспериментальной проверки СТО, или в экспериментах на основе эффекта Мессбауэра) значение частоты, отличающееся от полученного в эйнштейновской СТО. Квадратичный член разложения по степеням малого параметра имеет в ТПВ противоположный знак. Измерив квадратичную поправку в «продольном эффекте Доплера», можно однозначно установить, справедливы ли предположения о структуре пространства – времени, заложенные в виде аксиом в основание теории. Итак, слово за «его величеством» опытом.

Перейдем теперь к главному – к уравнениям поля ТПВ. Начнем с формулировки теоремы Э. Шредингера (E. Schrodinger), которая является исходной точкой для формального построения ТПВ. В книге Э. Шредингера [1] формулируется и доказывается следующая теорема:
Теорема Шредингера
Примитивная Г-метрика для несимметричной афинной связности Гkij и gij – метрика Римана согласованы в определенном смысле (см. [1]) тогда и только тогда, когда афинная связность имеет вид:

(2)
Итак, несимметричная аффинная связность (2) целиком определяется 10 независимыми компонентами метрического тензора ij и 20 независимыми компонентами тензора Tsij. Теперь сделаем следующее предположение, которое еще более конкретизирует аффинную связность и уменьшит число неизвестных функций. Утверждается, что тензор Tsij имеет вид:

(6)
где Vi(m) – касательный к геодезической вектор («вектор скорости»). Здесь требуется пояснить, как вводятся четыре (m = 0, 1, 2, 3) касательных вектора. В каждой точке 4-пространства можно задать четыре «взаимно ортогональные» геодезические линии: xk(m) = xk(m)( ) , касательные векторы к которым удовлетворяют уравнениям:
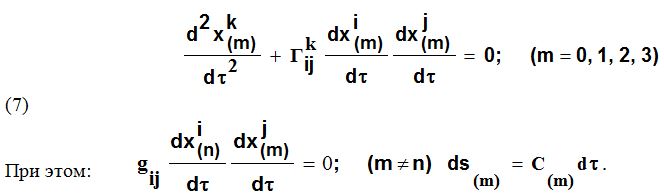
Физическое содержание четырех тензорных полей (6) чрезвычайно интересно и важно для понимания ТПВ. Первое, что приходит на ум, попытаться связать эти тензорные величины с электромагнитным полем, а точнее, с четырьмя электромагнитными полями в соответствующих им 3-пространствах. В любой точке 4-пространства существуют четыре вектора Vi(m) – касательных к геодезическим линиям Xi(m) = Xi(m)( ). Ортогональные к векторам дополнения – это трехмерные пространства, для которых касательные вектора Vi(m) в каждой точке задают направление времени. Одним из этих четырех трехмерных пространств является наше трехмерное пространство, допустим для определенности с индексом m = 0, в котором направление временной оси в каждой его точке P задается вектором Vi(0)(P). Опуская подробности, утверждается что уравнения классической электродинамики могут быть записаны в виде:

Утверждается также, что 16 уравнений (8) можно записать в трехмерной форме либо как «Первые пары уравнений Максвелла», либо как «Вторые пары уравнений Максвелла» и даже как «Материальные уравнения» для каждого из четырех 3-пространств. Иными словами, в электродинамике ТПВ обе пары уравнений Максвелла неразличимы и 16 уравнений электродинамики устанавливают связь между компонентами: B(m), E(m), с одной стороны, и H(m), D(m) – с другой (здесь: ![]() ).
).
Уравнения (8) в правой части не содержат плотности 4-тока. Иначе говоря, вид уравнений электродинамики такой, как если бы они были записаны для «пустого пространства», в котором нет ни зарядов, ни токов. Это обстоятельство позволяет, как минимум, надеяться, что при решении уравнений поля удастся избежать появления особенностей для точек пространства с «источниками поля». Последнее в принципе немыслимо для тех теорий, которые включают в свои полевые уравнения члены, описывающие источники поля. В ТПВ заряды и токи появляются только при переходе от четырехмерного описания единого грави-электромагнитного поля к трехмерным описаниям электромагнитных полей в каждом из четырех трехмерных подпространств. Плотности заряда и тока в нашем случае представляют собой исключительно трехмерные объекты.
Уравнения поля ТПВ
Уравнения поля получим исходя из вариационного принципа:

(11)
Учитывая тензорный характер уравнений (11), обращаем внимание на то, что все фигурирующие далее равенства являются исключительно тензорными соотношениями, хотя содержат не ковариантные, а обычные частные производные.
Представим тензор Риччи Rij относительно несимметричной афинной связности (4) в виде: Rij = Gij + Kij, где Gij – тензор Риччи, построенный из тензора кривизны Римана – Кристоффеля относительно метрической (кристоффелевой) связности. Можно показать, что в этом случае имеет место равенство (12), которое после подстановки в (11) приводит к уравнениям поля в форме (13):


(16)
В завключение позволим себе коротко прокомментировать полученный результат.
Во-первых, уравнения поля могут быть формально записаны в форме (15) хорошо известной системы уравнений ОТО с так называемым «космологическим лямбда-членом». Однако, в отличие от ОТО, в правой части равенства (15) присутствует член, имеющий чисто геометрическую природу (который по аналогии с ОТО назван «тензором материи»). Кроме того, коэффициент лямбда (16) не является в общем случае константой, а следовательно, речь не идет о пространстве ПОСТОЯННОЙ кривизны.
Как известно, эйнштейновская ОТО в этом месте испытывает некоторое «затруднение»: введение в уравнения поля ОТО лямбда-члена автоматически означает переход к пространству постоянной кривизны, что в свою очередь делает бессмысленным разговор о гравитационном поле в малом (не космологическом) объеме, т. е. в локальной области пространства с гравитирующей массой.

Что это означает, комментировать не нужно. Осталось в знаменитом «лифте Эйнштейна» построить генератор электромагнитных полей (6) и назвать этот лифт «летающей тарелкой».
Литература
1. Шредингер Э. Пространственно-временная структура вселенной / Под ред. Р.А. Асанова. – М.: Наука, 1986.
2. Джеммер М. Понятие массы в классической и современной физике. – М.: Прогресс, 1967.
3. Дирак П.А.М. Воспоминания о необычной эпохе: Сб. статей / Под ред. Я.А. Смородинского. – М.: Наука, 1990.
4. Эйнштейн А. Собрание научных трудов: В 4 т. Т. I, II / Под ред. И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: Наука, 1965.
5. Бёрке В.Л. Пространство – время. Геометрия. Космология. – М., 1980.