Н.С. Келлин
СПЕКТРАЛЬНЫЕ СВОЙСТВА ОПЕРАТОРА ПЕРЕНОСА ЧАСТИЦ
Изучается спектр оператора переноса частиц, отвечающего за описание их движения и поглощения (но не воспроизводства их в соударениях) в линеаризованном уравнении Больцмана. Вкупе с соответствующими начальными и граничными условиями оно описывает процесс переноса частиц самой различной природы (от нейтронов или фотонов в ядерных реакторах или в звёздных атмосферах, соответственно, до клеток в популяциях).
N.S. Kellin
PARTICAL TRANSPORT OPERATOR’S SPECTRAL PROPERTIES
The spectrum of particles transport operator which describes their motion and adsorption (without generation) in linearized Boltzmann equation is investigated in this paper. Together with corresponding initial and boundary conditions this equation describes many processes of particle transport (from neutrons and photons in nuclear reactors and star’s atmospheres correspondingly till cells in growing populations).
Введение
Задачи, связанные с анализом свойств оператора переноса частиц, рассматривались многими авторами. Например, в работе [1] было проведено исчерпывающее исследование односкоростной стационарной задачи переноса частиц в возможно невыпуклом теле, погружённом в вакуум. В работе [2] были сняты некоторые ограничения по стационарности и фиксированности модуля скорости частиц, но рассмотрение велось исключительно для выпуклых тел. Видимо, в работе автора [3] была сделана первая попытка провести соответствующий анализ для случая переноса частиц в компактном теле. В дальнейшем (лет на 20) интересы в теории переноса сместились в сторону численных исследований.
В настоящее время актуальность теоретического (функционально-аналитического) подхода к задачам теории переноса частиц вновь возрастает, что связано с заметным расширением области приложений (см., например, работу [4], где указана соответствующая литература). Рассмотрение переноса частиц проводится сейчас чаще всего [5, 6] не в модели В.С. Владимирова (тело погружено в вакуум), а в более простой модели К.О. Фридрихса (тело погружено в абсолютно чёрный поглотитель частиц [7]). В настоящей работе «реанимируется» модель Владимирова.
1. Постановка задачи

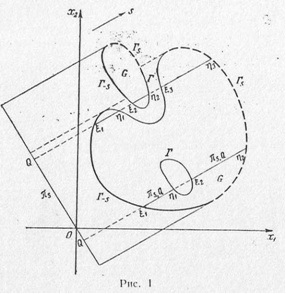




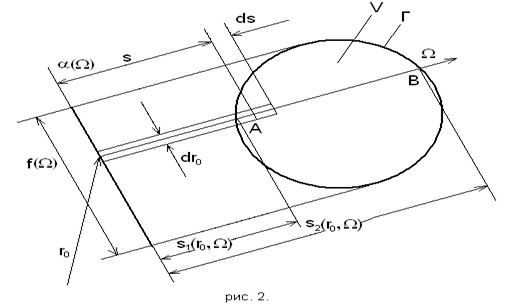





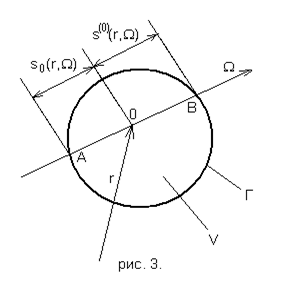
2. Результаты


10. Теорема показывает, в частности, эквивалентность стандартного подхода к спектральному анализу оператора переноса в комплексных пространствах, в рамках которого сопряженность операторов рассматривается относительно сопряженно-линейных (полуторалинейных) функционалов, и спектры операторов Â и Â+ получаются сопряженными друг другу, подходу, избранному в работе [2], при котором сопряженность операторов рассматривается относительно линейных функционалов, и, когда имеет место равенство спектральных множеств σ(Â)= σ(Â+).
Литература
1. Владимиров B.C. Математические задачи односкоростной теории переноса частиц, Тр. МИАН СССР им. В.А. Стеклова. Т.61. – М., 1961.
2. Шихов С.Б. Вопросы математической теории реакторов. Линейный анализ. – М.: Атомиздат, 1973.
3. Келлин Н.С. Анализ линейного уравнения Больцмана. Применение к теории переноса частиц. Дисс. … канд. физ.-мат. Наук. – М.: ИПМ АН СССР, 1985. – 140с.
4. Келлин Н.С., С.В.Паротькин Одномерная задача для системы уравнений Власова–Максвелла // Вестник МГОУ. Серия «Физика-математика». 2008. № 1. С. 36–45.
5. Стёпин С.А. Волновые операторы для линеаризованного уравнения Больцмана в односкоростной теории переноса // Матем. сб. 2001. № 1. С. 139–160.
6. Стёпин С.А. О модели Фридрихса в односкоростной теории переноса // Функ. ан. 2001. 35:2. С. 87–92.
7. Рихтмайер Р. Принципы современной математической физики. Т. 1–2. – М.: Мир, 1984.
8. Келлин Н.С. Оператор переноса частиц в пространствах Лебега, Рукопись депонирована в ВИНИТИ 3 декабря 1984 г., №7649/84 – Деп.
9. Келлин Н.С. Газокинетический оператор в пространствах Лебега. Рукопись депонирована в ВИНИТИ, 20 ноября 1984 г., №7401/84 – Деп.
10. Хилле Э., Филлипс Р. Функциональный анализ и полугруппы. – М.: Мир, 1972.
11. Като Т. Теория возмущений линейных операторов. – М.: Мир, 1972